While these lessons primarily focus on actuator devices such as motors, heaters, light sources, and other "output devices," many circuits employing actuator devices also incorporate sensors to monitor the behavior of these actuator devices. A characteristic example is a thermostat-controlled heater, where the control of the heating element's power is based on readings from a temperature sensor. Such control can involve simple on/off switching of the element or may rely on more advanced technology, such as the so-called proportional-integral-derivative (PID) control.
This chapter addresses the integration of sensors and actuator devices to create a control system. This technology will be applied to enhance the previously implemented beverage cooler project.
Control loops
Using a transistor to toggle power on and off allows achieving a high-speed switching process and harnessing Pulse Width Modulation (PWM) technology. However, for certain systems, frequent power cycling of a device is highly undesirable. This can apply to household heaters that require time to start generating heat after being powered on. Furthermore, controlling them using electromechanical switches and similar devices in constant on/off mode can shorten the heater's lifespan.
To prevent excessively rapid switching, it is necessary to set a minimum time during which the device cannot be turned off or introduce hysteresis.
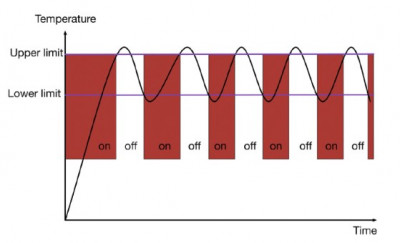
Applied to a thermostat, hysteresis means having not just one but two temperature thresholds, one of which is higher than the other by a fixed amount. If the temperature drops below the lower threshold, the heater turns on, but it only turns off when the temperature exceeds the upper threshold. Thus, the natural inertia of the system is used to introduce a delay in the switching process.
To prevent excessively rapid switching, it is necessary to set a minimum time during which the device cannot be turned off or introduce hysteresis.
Applied to a thermostat, hysteresis means having not just one but two temperature thresholds, one of which is higher than the other by a fixed amount. If the temperature drops below the lower threshold, the heater turns on, but it only turns off when the temperature exceeds the upper threshold. Thus, the natural inertia of the system is used to introduce a delay in the switching process.
Turning off the heater when the temperature sensor indicates that the heater is hotter than the set temperature and turning it on when it's cooler than that leads to a system where the temperature "oscillates" around the set value.
For more precise temperature control, proportional-integral-derivative (PID) control should be used.
Instead of simply turning the heater on and off, a PID controller regulates the output power of the heater (or another actuator) taking into account three factors: proportional, integral, and derivative.
[Warning]
[In this section, we will dive deeper into the theory. Questions about PID control are quite common, and one of the main goals I've chosen is to explain the principles and applications of PID control.]
Proportional (P)
Using only the P-part of the PID controller and ignoring the other two - I and D, can yield quite good results on many systems. Therefore, on every new system, it's advisable to start with only the P-part and see how acceptable the results turn out.
Proportional control means that the power supplied to the heater is proportional to the error. The greater the error, i.e., the lower the actual temperature compared to the set temperature, the more power is supplied to the heater. As the actual temperature approaches the set temperature, the power decreases, resulting in the actual temperature not exceeding the set one as much as shown in the "temperature graph of a simple thermostat working on an on/off basis." Depending on the system, it will likely still exceed the set temperature, but not as much as it would with simple on/off control. This process is somewhat akin to approaching a stop sign while driving – you begin to slow down in advance, not right at the sign itself.
If the actual temperature is higher than the set temperature, the error will be negative, and this should result in reducing the power to the heater. If the heater were a Peltier element, you could use an H-bridge to send current through it in the opposite direction and turn it from a heater into a cooler. However, in practice, unless the ambient temperature significantly differs from the set temperature, there's no need to do that. Instead, you can simply let the system naturally cool down (or heat up).
The discrepancy used in calculating the output power in the case of a thermostat is the temperature difference. Expressing it in degrees Celsius, if the set temperature is 30°C and the measured temperature is 25°C, then the discrepancy is 5°C (30°C - 25°C). If a Pulse Width Modulation (PWM) scheme is used with an Arduino for setting the output, the output will range from 0 to 255. Therefore, directly setting the discrepancy value (5) would result in providing too little power to the heater, which is likely insufficient to raise the temperature to 30°C. Hence, to obtain the value of the applied output power, the discrepancy is multiplied by a number called kp (sometimes referred to as "gain" as well). Changing kp determines how quickly the temperature will rise to the set value. With a low kp value, the temperature may never reach the desired level, but with a very high kp value, the system will behave similarly to a simple on/off temperature controller, causing the actual temperature to oscillate around the set temperature. The figure below illustrates how different values of kp affect the behavior of an idealized system.
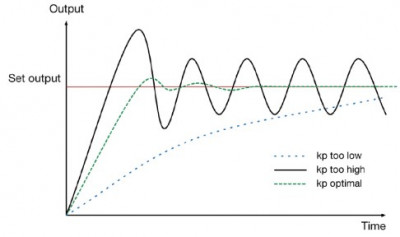
Here, it can be observed that if the value of kp is too low, the temperature may never reach the desired level, or it may take too long to do so. On the other hand, if the value of kp is too high, oscillations will occur at the output, and their magnitude will not decrease. The appropriate value of kp will quickly adjust the output to the desired level, perhaps with a slight overshoot, and then the oscillations will quickly settle to an acceptably low level.
Finding the suitable value of kp is referred to as system tuning. Tuning of PID control will be discussed further.
Returning to the example with a set temperature of 30°C but an actual temperature of 25°C, in this case, it is still desirable for the heater to dissipate the maximum power, i.e., a PWM duty cycle of 255 (100%). If a value of 50 is chosen for kp, then a discrepancy of 5 units will lead to the following output power:
Output = Discrepancy x kp = 5 x 50 = 250
Once the system is only 1°C away from the set temperature, the output power will decrease to the following value:
Output = Discrepancy x kp = 1 x 50 = 50
This power may be sufficient or insufficient for the system to reach the desired temperature. Systems vary, so the controller requires tuning.
Integral (I)
If achieving the required precision of power control through proportional control is not possible, calculations may require the addition of a value I to calculate the output power using the following formula:
Output = Discrepancy x kp + I x ki.
Here, a new constant ki is introduced, scaling our new mysterious property called "I" (let's reveal the secret - it's precisely Integral), and the output power is calculated by adding this integral component to the previously discussed proportional component. This type of controller is called a PI controller (PI, or sometimes P + I, don't confuse it with "Pi" in Raspberry Pi). Both the use of a purely proportional controller and a PI controller sometimes yield quite acceptable results, eliminating the need to add the third component of the PID controller, D.
The integral component is calculated by maintaining the current sum of discrepancies with each temperature measurement. When the discrepancy is positive (heating), the I-component will continue to increase, exceeding the value of the initial response. Reduction will only start when the discrepancy becomes negative after exceeding the set temperature.
Once the actual temperature reaches the set temperature, the I-component has a calming effect, smoothing out temperature changes to better maintain the temperature at the desired value.
The only problem with the I-component is that it provides a large boost as the temperature rises, potentially leading to a significant temperature overshoot, after which time is required for it to decrease to the set temperature and stabilize.
Derivative (D)
In practice, the D-component is often not used in real control systems because the benefits of using it to reduce overshoots are outweighed by the complexity of tuning.
When adding the D-component to the control program to counteract overshoot effects, the output power is calculated using the following formula:
Output = Discrepancy x kp + I x ki + D x kd.
The D-component measures how quickly the discrepancy changes between each temperature measurement, and therefore, it somewhat predicts where the temperature is heading.
PID Controller Tuning
Tuning a PID controller involves finding values for kp, ki, and kd that make the system behave appropriately. I recommend simplifying things and using only PI control, setting kd to zero. Then, you only need to tune two parameters. In fact, this simplification eases the tuning process for most systems, although it slightly increases the time spent on tuning.
In the section "Experiment: Thermostatic PID Controller," I will guide you through a trial-and-error method that works well for the temperatures the controller deals with. The rest of the section will focus on the most popular method of PID tuning known as the Ziegler-Nichols method. This method significantly streamlines the process of obtaining values for kp, ki, and kd, reducing it to a series of experiments followed by straightforward calculations.
Ziegler-Nichols tuning starts with setting ki and kd to zero in order for the controller to work in proportional mode. Then, the kp value is gradually increased until the output power starts to oscillate. The kp value at which this happens is called ku.
After determining the value of ku, you need to measure the number of oscillations per second (oscillation period, referred to as pu).
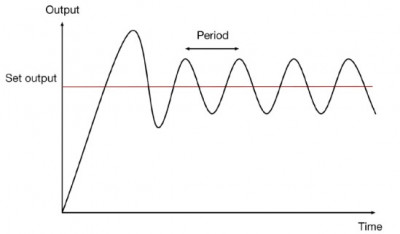
To obtain it, you should plot the power readings on the load, as was done in the experiment in the section "Experiment: How Good Is a Thermostat Based on On/Off Control?"
Then, you can calculate the values for kp, ki, and kd:
kp = 0.6 x ku
ki = (2 x ku) / pu
kd = (ku x pu) / 8
If you are using a PI controller, it is better to use the following calculations:
ku = 0.45 x ku
ki = (1.2 x kp) / pu
kd = 0
You can find an article on the Ziegler-Nichols method in Wikipedia (http://en.wikipedia.org/wiki/PID_controller).
For more precise temperature control, proportional-integral-derivative (PID) control should be used.
Instead of simply turning the heater on and off, a PID controller regulates the output power of the heater (or another actuator) taking into account three factors: proportional, integral, and derivative.
[Warning]
[In this section, we will dive deeper into the theory. Questions about PID control are quite common, and one of the main goals I've chosen is to explain the principles and applications of PID control.]
Proportional (P)
Using only the P-part of the PID controller and ignoring the other two - I and D, can yield quite good results on many systems. Therefore, on every new system, it's advisable to start with only the P-part and see how acceptable the results turn out.
Proportional control means that the power supplied to the heater is proportional to the error. The greater the error, i.e., the lower the actual temperature compared to the set temperature, the more power is supplied to the heater. As the actual temperature approaches the set temperature, the power decreases, resulting in the actual temperature not exceeding the set one as much as shown in the "temperature graph of a simple thermostat working on an on/off basis." Depending on the system, it will likely still exceed the set temperature, but not as much as it would with simple on/off control. This process is somewhat akin to approaching a stop sign while driving – you begin to slow down in advance, not right at the sign itself.
If the actual temperature is higher than the set temperature, the error will be negative, and this should result in reducing the power to the heater. If the heater were a Peltier element, you could use an H-bridge to send current through it in the opposite direction and turn it from a heater into a cooler. However, in practice, unless the ambient temperature significantly differs from the set temperature, there's no need to do that. Instead, you can simply let the system naturally cool down (or heat up).
The discrepancy used in calculating the output power in the case of a thermostat is the temperature difference. Expressing it in degrees Celsius, if the set temperature is 30°C and the measured temperature is 25°C, then the discrepancy is 5°C (30°C - 25°C). If a Pulse Width Modulation (PWM) scheme is used with an Arduino for setting the output, the output will range from 0 to 255. Therefore, directly setting the discrepancy value (5) would result in providing too little power to the heater, which is likely insufficient to raise the temperature to 30°C. Hence, to obtain the value of the applied output power, the discrepancy is multiplied by a number called kp (sometimes referred to as "gain" as well). Changing kp determines how quickly the temperature will rise to the set value. With a low kp value, the temperature may never reach the desired level, but with a very high kp value, the system will behave similarly to a simple on/off temperature controller, causing the actual temperature to oscillate around the set temperature. The figure below illustrates how different values of kp affect the behavior of an idealized system.
Here, it can be observed that if the value of kp is too low, the temperature may never reach the desired level, or it may take too long to do so. On the other hand, if the value of kp is too high, oscillations will occur at the output, and their magnitude will not decrease. The appropriate value of kp will quickly adjust the output to the desired level, perhaps with a slight overshoot, and then the oscillations will quickly settle to an acceptably low level.
Finding the suitable value of kp is referred to as system tuning. Tuning of PID control will be discussed further.
Returning to the example with a set temperature of 30°C but an actual temperature of 25°C, in this case, it is still desirable for the heater to dissipate the maximum power, i.e., a PWM duty cycle of 255 (100%). If a value of 50 is chosen for kp, then a discrepancy of 5 units will lead to the following output power:
Output = Discrepancy x kp = 5 x 50 = 250
Once the system is only 1°C away from the set temperature, the output power will decrease to the following value:
Output = Discrepancy x kp = 1 x 50 = 50
This power may be sufficient or insufficient for the system to reach the desired temperature. Systems vary, so the controller requires tuning.
Integral (I)
If achieving the required precision of power control through proportional control is not possible, calculations may require the addition of a value I to calculate the output power using the following formula:
Output = Discrepancy x kp + I x ki.
Here, a new constant ki is introduced, scaling our new mysterious property called "I" (let's reveal the secret - it's precisely Integral), and the output power is calculated by adding this integral component to the previously discussed proportional component. This type of controller is called a PI controller (PI, or sometimes P + I, don't confuse it with "Pi" in Raspberry Pi). Both the use of a purely proportional controller and a PI controller sometimes yield quite acceptable results, eliminating the need to add the third component of the PID controller, D.
The integral component is calculated by maintaining the current sum of discrepancies with each temperature measurement. When the discrepancy is positive (heating), the I-component will continue to increase, exceeding the value of the initial response. Reduction will only start when the discrepancy becomes negative after exceeding the set temperature.
Once the actual temperature reaches the set temperature, the I-component has a calming effect, smoothing out temperature changes to better maintain the temperature at the desired value.
The only problem with the I-component is that it provides a large boost as the temperature rises, potentially leading to a significant temperature overshoot, after which time is required for it to decrease to the set temperature and stabilize.
Derivative (D)
In practice, the D-component is often not used in real control systems because the benefits of using it to reduce overshoots are outweighed by the complexity of tuning.
When adding the D-component to the control program to counteract overshoot effects, the output power is calculated using the following formula:
Output = Discrepancy x kp + I x ki + D x kd.
The D-component measures how quickly the discrepancy changes between each temperature measurement, and therefore, it somewhat predicts where the temperature is heading.
PID Controller Tuning
Tuning a PID controller involves finding values for kp, ki, and kd that make the system behave appropriately. I recommend simplifying things and using only PI control, setting kd to zero. Then, you only need to tune two parameters. In fact, this simplification eases the tuning process for most systems, although it slightly increases the time spent on tuning.
In the section "Experiment: Thermostatic PID Controller," I will guide you through a trial-and-error method that works well for the temperatures the controller deals with. The rest of the section will focus on the most popular method of PID tuning known as the Ziegler-Nichols method. This method significantly streamlines the process of obtaining values for kp, ki, and kd, reducing it to a series of experiments followed by straightforward calculations.
Ziegler-Nichols tuning starts with setting ki and kd to zero in order for the controller to work in proportional mode. Then, the kp value is gradually increased until the output power starts to oscillate. The kp value at which this happens is called ku.
After determining the value of ku, you need to measure the number of oscillations per second (oscillation period, referred to as pu).
To obtain it, you should plot the power readings on the load, as was done in the experiment in the section "Experiment: How Good Is a Thermostat Based on On/Off Control?"
Then, you can calculate the values for kp, ki, and kd:
kp = 0.6 x ku
ki = (2 x ku) / pu
kd = (ku x pu) / 8
If you are using a PI controller, it is better to use the following calculations:
ku = 0.45 x ku
ki = (1.2 x kp) / pu
kd = 0
You can find an article on the Ziegler-Nichols method in Wikipedia (http://en.wikipedia.org/wiki/PID_controller).
PID Controller Experiment
In this experiment, we will explore the operation of a PID controller using both Arduino and Raspberry Pi. The program for the PID controller using Arduino is taken from the library, while the program for the PID controller using Raspberry Pi will need to be manually typed.
Equipment
This experiment uses the exact same equipment as the experiment in the section "Experiment: How Good is an On/Off Thermostat?" However, when connecting it to the Raspberry Pi, special attention must be paid because the DS18B20 chip and the resistor-based heater should be powered separately: power the DS18B20 chip with a 3.3V voltage and the resistor heater with a 5V voltage. This is because the digital output from DS18B20 should rise to 3.3V, not 5V, to avoid damaging the input circuits of Raspberry Pi.
Raspberry Pi Connection
The circuit assembled on the Raspberry Pi's breadboard differs slightly from what was assembled for Arduino. The key difference is that we need the resistive heater to still operate at 5V, and for the DS18B20 temperature sensor to be compatible with Raspberry Pi's GPIO pins, it needs to operate at 3.3V.

Raspberry Pi Program
To make the DS18B20 chip work with the Raspberry Pi, some preparation is required. First, you need to enable the 1-Wire bus. Edit the /boot/config.txt file using the following command:
$ sudo nano /boot/config.txt
Add the following line to the end of the file:
dtoverlay=w1-gpio
Now, you need to restart the Raspberry Pi for the changes to take effect. The DS18B20 chip uses a text file-like interface, so the Python program will need to read the file and extract temperature measurements from it. You can try doing this before running the entire program to see what the message format looks like. Navigate to the /sys/bus/w1/devices directory with the following command:
$ cd /sys/bus/w1/devices
Then, list the directories in this folder using the following command:
$ ls
28-000002ecba60 w1_bus_master1
pi@raspberrypi /sys/bus/w1/devices $
Make the directory whose name starts with 28 the current directory. In our case, it's the directory 28-000002ecba60 (yours will likely have a different name):
$ cd 28-000002ecba60
Finally, run the following command to extract the most recent temperature readings:
$ cat w1_slave
The response comes in two lines:
53 01 4b 46 7f ff Od 10 e9 : crc=e9 YES
53 01 46 46 71 ff od 10 e9 t=21187
pi@raspberrypi /sys/bus/w1/devices/28-000002ecba60 $
The first part of each line is a unique identifier for the temperature sensor, and the first line ends with the word "YES," indicating a successful reading. The second line ends with the temperature reading, expressed in thousandths of a degree Celsius. In this case, it's 21,187 (or 21.187°C).
While there are available Python libraries for PID control, they are more complex to use than their Arduino counterparts. Therefore, for the Raspberry Pi version, the PID algorithm will be implemented from scratch (though some inspiration was drawn from the Arduino library, aiming to make the two versions as similar as possible). Let's clarify some aspects of the program step by step, using the comments in the code:
1. This code determines the directory where the DS18B20 file is located. It's done almost the same way as in the previously discussed method, using the glob command to find the first directory starting with 28.
2. These global variables are used by the PID algorithm. The old_error variable is used to calculate the change in error for the D component.
3. The read_temp function reads the DS18820 sensor readings in the form of two text lines.
4. The read_temp function is responsible for actually extracting the temperature reading from the end of the second line after checking that the first line received a "YES" response.
5. This auxiliary function limits the value of its first parameter to always be within the range specified by the second and third parameters.
6. The update_pid function contains the PID calculation code.
7. Calculation of dt (how much time has passed since the last call to the update_pid function).
8. Calculation of the error.
9. Calculation of the change in error de.
10. Calculation of the proportional component.
11. Adding the current value of error * ki to i_term.
12. Limiting the range of i_term to the same range as the output (0 to 100).
13. Calculation of d_term.
14. Summing up all the components and limiting the value range to the output range from 0 to 100.
15. Unlike the Arduino version, which allows tuning the tuning parameters while the controller is running, the Python program makes a one-time request for temperature, kp, ki, and kd.
16. The old_time variable is initialized with the current time just before the main control loop starts.
17. If 1 second has passed since the last measurement, it measures the temperature, gets a new output value (duty), and adjusts the PWM channel accordingly.
Uploading and Running the Program
One of the differences between the Arduino version of the program and the Raspberry Pi version is that Raspberry Pi's output range is from 0 to 100, while Arduino's is from 0 to 255. Therefore, the kp and ki values found during Arduino setup need adjustment for Raspberry Pi. Essentially, to fit the output into the 0-100 range, you can simply divide the kp and ki values by 2.5. This would result in a kp value of 280 and a ki value of 22.
Run the program, set the temperature to 30, and input these numbers, and you should obtain data similar to what was achieved using the Arduino version:
$ sudo python ex_11_pid_thermostat.py
Enter the target temperature in degrees Celsius 30
kp: 280
ki: 22
kd: 0
23.437, 30, 100 23.437, 30, 100
23.5, 30, 100 23.562, 30, 100
23.687, 30, 100
Plotting these figures using a spreadsheet, I got the results shown in the figure. This also uses a stretched representation of the temperature, which is adjusted quite precisely.

In this experiment, we will explore the operation of a PID controller using both Arduino and Raspberry Pi. The program for the PID controller using Arduino is taken from the library, while the program for the PID controller using Raspberry Pi will need to be manually typed.
Equipment
This experiment uses the exact same equipment as the experiment in the section "Experiment: How Good is an On/Off Thermostat?" However, when connecting it to the Raspberry Pi, special attention must be paid because the DS18B20 chip and the resistor-based heater should be powered separately: power the DS18B20 chip with a 3.3V voltage and the resistor heater with a 5V voltage. This is because the digital output from DS18B20 should rise to 3.3V, not 5V, to avoid damaging the input circuits of Raspberry Pi.
Raspberry Pi Connection
The circuit assembled on the Raspberry Pi's breadboard differs slightly from what was assembled for Arduino. The key difference is that we need the resistive heater to still operate at 5V, and for the DS18B20 temperature sensor to be compatible with Raspberry Pi's GPIO pins, it needs to operate at 3.3V.
Raspberry Pi Program
To make the DS18B20 chip work with the Raspberry Pi, some preparation is required. First, you need to enable the 1-Wire bus. Edit the /boot/config.txt file using the following command:
$ sudo nano /boot/config.txt
Add the following line to the end of the file:
dtoverlay=w1-gpio
Now, you need to restart the Raspberry Pi for the changes to take effect. The DS18B20 chip uses a text file-like interface, so the Python program will need to read the file and extract temperature measurements from it. You can try doing this before running the entire program to see what the message format looks like. Navigate to the /sys/bus/w1/devices directory with the following command:
$ cd /sys/bus/w1/devices
Then, list the directories in this folder using the following command:
$ ls
28-000002ecba60 w1_bus_master1
pi@raspberrypi /sys/bus/w1/devices $
Make the directory whose name starts with 28 the current directory. In our case, it's the directory 28-000002ecba60 (yours will likely have a different name):
$ cd 28-000002ecba60
Finally, run the following command to extract the most recent temperature readings:
$ cat w1_slave
The response comes in two lines:
53 01 4b 46 7f ff Od 10 e9 : crc=e9 YES
53 01 46 46 71 ff od 10 e9 t=21187
pi@raspberrypi /sys/bus/w1/devices/28-000002ecba60 $
The first part of each line is a unique identifier for the temperature sensor, and the first line ends with the word "YES," indicating a successful reading. The second line ends with the temperature reading, expressed in thousandths of a degree Celsius. In this case, it's 21,187 (or 21.187°C).
While there are available Python libraries for PID control, they are more complex to use than their Arduino counterparts. Therefore, for the Raspberry Pi version, the PID algorithm will be implemented from scratch (though some inspiration was drawn from the Arduino library, aiming to make the two versions as similar as possible). Let's clarify some aspects of the program step by step, using the comments in the code:
Code: Select all
import os
import glob
import time
import RPi.GPIO as GPIO
GPIO.setmode(GPIO.BCM)
heat_pin = 18
base_dir = '/sys/bus/w1/devices/' # (1)
device_folder = glob.glob(base_dir + '28*')[0]
device_file = device_folder + '/w1_slave'
GPIO.setup(heat_pin, GPIO.OUT)
heat_pwm = GPIO.PWM(heat_pin, 500)
heat_pwm.start(0)
old_error = 0 # (2)
old_time = 0
measured_temp = 0
p_term = 0
i_term = 0
d_term = 0
def read_temp_raw(): # (3)
f = open(device_file, 'r')
lines = f.readlines()
f.close()
return lines
def read_temp(): # (4)
lines = read_temp_raw()
while lines[0].strip()[-3:] != 'YES':
time.sleep(0.2)
lines = read_temp_raw()
equals_pos = lines[1].find('t=')
if equals_pos != -1:
temp_string = lines[1][equals_pos+2:]
temp_c = float(temp_string) / 1000.0
return temp_c
def constrain(value, min, max): # (5)
if value < min :
return min
if value > max :
return max
else:
return value
def update_pid(): # (6)
global old_time, old_error, measured_temp, set_temp
global p_term, i_term, d_term
now = time.time()
dt = now - old_time # (7)
error = set_temp - measured_temp # (8)
de = error - old_error # (9)
p_term = kp * error # (10)
i_term += ki * error # (11)
i_term = constrain(i_term, 0, 100) # (12)
d_term = (de / dt) * kd # (13)
old_error = error
# print((measured_temp, p_term, i_term, d_term))
output = p_term + i_term + d_term # (14)
output = constrain(output, 0, 100)
return output
set_temp = input('Enter set temperature in C ') # (15)
kp = input('kp: ')
ki = input('ki: ')
kd = input('kd: ')
old_time = time.time() # (16)
try:
while True:
now = time.time()
if now > old_time + 1 : # ()17)
old_time = now
measured_temp = read_temp()
duty = update_pid()
heat_pwm.ChangeDutyCycle(duty)
print(str(measured_temp) + ', ' + str(set_temp) + ', ' + str(duty))
finally:
GPIO.cleanup()2. These global variables are used by the PID algorithm. The old_error variable is used to calculate the change in error for the D component.
3. The read_temp function reads the DS18820 sensor readings in the form of two text lines.
4. The read_temp function is responsible for actually extracting the temperature reading from the end of the second line after checking that the first line received a "YES" response.
5. This auxiliary function limits the value of its first parameter to always be within the range specified by the second and third parameters.
6. The update_pid function contains the PID calculation code.
7. Calculation of dt (how much time has passed since the last call to the update_pid function).
8. Calculation of the error.
9. Calculation of the change in error de.
10. Calculation of the proportional component.
11. Adding the current value of error * ki to i_term.
12. Limiting the range of i_term to the same range as the output (0 to 100).
13. Calculation of d_term.
14. Summing up all the components and limiting the value range to the output range from 0 to 100.
15. Unlike the Arduino version, which allows tuning the tuning parameters while the controller is running, the Python program makes a one-time request for temperature, kp, ki, and kd.
16. The old_time variable is initialized with the current time just before the main control loop starts.
17. If 1 second has passed since the last measurement, it measures the temperature, gets a new output value (duty), and adjusts the PWM channel accordingly.
Uploading and Running the Program
One of the differences between the Arduino version of the program and the Raspberry Pi version is that Raspberry Pi's output range is from 0 to 100, while Arduino's is from 0 to 255. Therefore, the kp and ki values found during Arduino setup need adjustment for Raspberry Pi. Essentially, to fit the output into the 0-100 range, you can simply divide the kp and ki values by 2.5. This would result in a kp value of 280 and a ki value of 22.
Run the program, set the temperature to 30, and input these numbers, and you should obtain data similar to what was achieved using the Arduino version:
$ sudo python ex_11_pid_thermostat.py
Enter the target temperature in degrees Celsius 30
kp: 280
ki: 22
kd: 0
23.437, 30, 100 23.437, 30, 100
23.5, 30, 100 23.562, 30, 100
23.687, 30, 100
Plotting these figures using a spreadsheet, I got the results shown in the figure. This also uses a stretched representation of the temperature, which is adjusted quite precisely.
In this project for Arduino, we will add thermostat control to the project from the section "Project: Beverage Cooler" so that beverages can be cooled more accurately to the desired temperature (as shown in the diagram below). In the future, the project will be further developed by adding a display showing the set and actual temperatures. As mentioned, this project is implemented using Arduino. However, if you have already learned how to use Raspberry Pi with the DS18B20 sensor, you should not have any problems adapting the project to work with Raspberry Pi as well.
viewtopic.php?p=179#p179
viewtopic.php?p=179#p179
